|
|
|
 |
|
|
| LIMDEP V8.0 |
|
 LIMDEP Windows 95/NT版 LIMDEP Windows 95/NT版
 スペック スペック
 LIMDEP7.0の機能と特徴 LIMDEP7.0の機能と特徴
 NLOGIT3.0 NLOGIT3.0
 Applications Applications
 LIMDEP V8.0のTopに戻る LIMDEP V8.0のTopに戻る
|
LIMDEP Version 7.0の機能と特徴
LIMDEP is the premier program for estimation and analysis of regression models, and qualititative and limited dependent variables.
No other program offers a greater variety of modelling frameworks, tools and features for analysis of cross section, panel, and time series data.
The following lists the main features of the program.
●Program Highlights
* Full Windows 95/NT API user interface
* Unlimited data set sizes
* Commands entered by dialog boxes and menus or by text editing
* Many tools for data entry, transformation, and file creation
* Approximately 100 fully automated modelling frameworks
* Matrix algebra, variable and scalar manipulation, and other programming tools
●Data Handling Procedures
LIMDEP allows you to analyze large data sets and large models. The active data set may contain up to 200 variables. The number of observations is unlimited; users have reported samples of up to one million observations.
Data entry may be from virtually any other program. LIMDEP can read rectangular ASCII files, binary files, and Lotus and Excel worksheet files. LIMDEP also contains its own data editor that allows you to edit the data in a window after importing them. A feature is provided for merging group invariant variables into panel data sets. Missing data are detected upon input, and may be bypassed automatically during estimation.
Data Input and Output
* Input using ASCII, .XLS, .WKS, binary, or .DIF file formats
* Formatted or unformatted data sets
* Missing data handling
* Panel data procedures
* Data file creation for export using all input formats
* File formats for export may be ASCII, binary, XLS, WKS
* Data may be exported directly to and imported from
spreadsheet programs
* Data conversion from real to integer
* Missing data indicated as isolated dots
* All data handled in double precision
(DOS version retains single precision)
Data Transformations
* All algebraic transformations of variables
* Special operators for dummy variables: (x=a) produces 1[x equal to a]
* Logical comparisons: IF( condition ) ... (ELSE) ... (ENDIF)
* Looping procedures allow transformations of a set of variables
* Fast sort, ascending or descending, carrying other variables
* Dozens of functions:
* Standard: Log, Exp, Abs, Sqr, Int, Fix, Sgn, Sin, Cos, Gma, Psi
* Normal distribution, N01, Phi, mean and variance for truncation
* Trends and group indicators
* Other distributions: bivariate normal, logistic, Poisson,
negative binomial, binomial
* Random number generators: normal, uniform, logistic, Poisson,
over 20 discrete and continuous distributions in all
* Multivariate normal probabilities using GHK simulation
Sample Definition
* Sample definition by specific observations
* Sample definition by dates for time series data
* Draw random samples from the data set, with or without replacement
* Sample restriction by conditions: (e.g., INCLUDE IF (Sex = 1 & Age > 18) )
* Automatic exclusion of observations with missing values
Variables Specification
* List names equated to collections of variables
* Logs and lagged values specified in commands
* Wildcard characters for sets of variables
●Descriptive Statistics
* Means, standard deviations, skewness, normality tests
* Stratification
* Order statistics and quantiles
* High resolution scatter plots
* Histograms and frequency plots, continuous or discrete data
* Crosstabulations
* Autocorrelations and partial autocorrelations
* Plots of user defined functions
* Normal-quantile plots

●Linear and Nonlinear Model Estimation
Linear Regression and Multiple Linear Equations Models
* All standard linear regression features
* Summary statistics, regression diagnostics
* AR models, GLS or MLS
* ARMAX models by nonlinear least squares
* 2SLS with autocorrelation
* 3SLS and SURE for up to 30 equations
* GLS and MLE for constrained SURE systems
* Residual plots, CUSUM tests, influence analysis
* Stepwise regression
* Restricted OLS or GLS
* Multiplicative heteroscedasticity
* Time series/cross section covariance structures
* Panel corrected standard errors
* White and Newey-West robust covariance matrices
* Box-Cox regression, GLS or MLE
* NIST benchmarks for accuracy, met to 10+ digits (files included)
Nonlinear Regression and Nonlinear Optimization
* Nonlinear least squares
* Nonlinear SURE for up to 20 equations
* Nonlinear 2SLS and 3SLS
* GMM estimation, up to 20 equations
* User defined ML estimation programs
* Variances and hypothesis tests for algebraically defined nonlinear functions of estimates
The following is one of the models in the National Institute
of Standards and Technology suite of benchmark programs for
assessing the accuracy of nonlinear least squares programs.
Model: 3 Parameters (b1 to b3)
y = b1 * (b2+x)**(-1/b3) + e
LIMDEP can estimate the model as is. But, it contains an
unnecessary nonlinearity, and can be estimated much more easily
by replacing -1/b3 with c3, then going back and recovering
the original parameter. The WALD command does the second
step with no extra programming on your part.
NLSQ;LHS=Y
;FCN= B1 * (B2+X)^C3
;LABELS=B1,B2,C3
;START= ... a list of values $
WALD;FN1=-1/C3$
WALD reports the estimate of b3 and an estimated standard error.
* MINIMIZE for user defined functions such as log-likelihoods
* Functions may include integration by quadrature
* Function integration
* Function differentiation
* User defined function plotting
* High accuracy on NIST benchmark test (test problems provided)
Models for Qualitative Dependent Variables
* Univariate and bivariate probit models
* Probit and logit models with multiplicative heteroscedasticity
* Binomial or multinomial logit
* Several specifications of partial observability models
* Probit with sample selectivity
* Conditional logit for discrete choice
* Fixed and random effects for both probit and logit models
* Nested logit models, FIML, up to four levels (with NLOGIT added)
* Heteroscedastic extreme value model
* Discrete choice with rank data
* Choice based sampling for all QDV models
* Ordered probit and logit
* Ordered probit with sample selection
* Individual or proportions data for all models
* Maximum score estimation
* Nonparametric estimation for binary response
* Random effects for ordered probit models
* Ordered probit and logit with stratified data
* Marginal effects computed automatically for all discrete choice models
* NEW! Multinomial and multivariate probit - up to 20 equations
Models for Discrete Choice (Multinomial Logit and Nested Logit Models)
With NLOGIT added, LIMDEP contains the most complete estimation package for multinomial and nested logit models available with any general econometrics program. Some of the features of NLOGIT are:
* Nested logit models with up to four levels and up to 85 choices
* Covariance heterogeneity models
* Random parameters logit model with fully correlated parameters
* Heteroscedastic extreme value model
* Multinomial probit model (up to 20 choices)
* Individual, frequencies, proportions, or ranks data
* Choice based sampling corrections
* Marginal effects computed by several different methods
* Full information maximum likelihood or sequential, limited information maximum likelihood estimation
* Predicted probabilities, utilities, and inclusive values
Models for Counts (Poisson and Negative Binomial)
* Poisson and negative binomial regression
* Models with truncation or censoring
* Models with altered probability of zero (ZIP models)
* Sample selection, by nonlinear least squares of FIML
* Normal heterogeneity and overdispersion
* Models with endogenous underreporting
* Models with normal heterogeneity and excess zeros
* Fixed and random effects models for panel data
* Semiparametric models for panel data with random effects
Limited Dependent Variable Models
* Tobit and truncated regression models
* Tobit model with multiplicative heteroscedasticity
* Left, right, or both tails censored with constant or variable limits
* Random effects models for truncated distributions
* Lognormal and truncated lognormal regression
* Nested tobit model
* Bivariate tobit model
* Tobit models with sample selection
* Grouped (completely censored) data regression
* Grouped data model with selection
Models for Sample Selection
* Linear Regression Model
* Two step LS or MLE
* Univariate or bivariate probit selection
* Selection by other kinds of models, e.g., tobit
* Marginal effects decomposition
* Switching regression models
* Treatment effects models
* Probit models with selectivity
* Poisson and negative binomial models with selectivity
Stochastic Frontier Models
* Half normal, truncated normal, or exponential distributions
* Random effects for panel data
* Estimates of one sided disturbance components
Duration and Survival Models
* Kaplan-Meier survival tables
* Cox proportional hazards model
* Stratified samples
* Weibull, lognormal, Gompertz, loglogistic, exponential, gamma parametric, Generalized F models
* Weibull and exponential models with gamma heterogeneity
* Arbitrary censoring and left truncation
* Time varying covariates
* Plots of survival, hazard, and integrated hazard functions
* Semiparametric hazard function estimation
* Split population survival models
Models for Panel Data (No other program provides a wider variety of specifications!)
* Linear regression with up to 20,000 groups
* Variable group sizes (unbalanced panels) for all models
* Random coefficients model with predictions of individual coefficient vectors
* TSCS covariance structures model
* Random effects probit model
* Random effects binary logit model
* Random effects tobit model
* Random effects stochastic frontier model
* Fixed effects binary logit model
* Random and fixed effects Poisson model (gamma or normal effects)
* Random and fixed effects negative binomial model
* Random effects ordered probit and logit models
●Tools and Programming Features
Matrix Algebra
In addition to the estimation programs, LIMDEP contains an extensive matrix programming language. The matrix processor can be used to program new estimation routines or to analyze data and matrices. There are dozens of functions with the familiar matrix operators, such as Root for characteristic roots (real or complex) and Dtrm (determinant). Operators are specified algebraically, with <matrix> or /matrix signifying inversion, * signifying multiplication, and so on. Matrix operations can also be made conditional on other results, using IF/ELSE/ENDIF constructions. Matrix programs operate with the results of other LIMDEP procedures. For example:
REGRESSION ; ... $
MATRIX ; IF( RSQRD > .5) | one set of computations
; (ELSE) | a different computation
; (ENDIF) | a third computation $
Data matrices can be defined just by collecting a list of variable names. The rows of the data matrix are defined by whatever sample observations you are using at the time. The matrix commands are not an add-on to the statistical programs; they are written to interact with them in a way that fully integrates your matrix commands and the model estimation programs. They are also written to allow manipulation of extremely large data matrices (up to one million observations). For the variables defined in a list named X, the symbols X'X and <X'X > produce a moment matrix and its inverse for an unlimited number of observations.
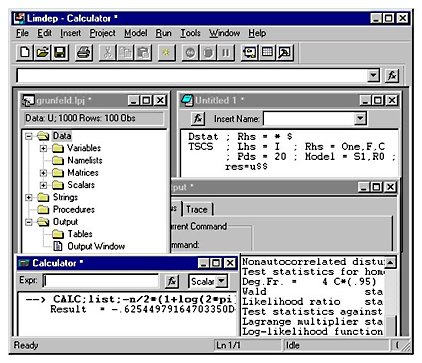
Scientific Calculator
LIMDEP also contains a powerful scientific calculator. The calculator can stand alone, for example, to replace all standard probability tables for the normal family, or it can be integrated into your statistical commands. (LIMDEP's inverse probability routines have been verified for accuracy to at least eight significant digits.) CALCULATE commands are also structured with LIMDEP's programming language using IF/ELSE/ENDIF.
Programming Structures
* PROCEDURE defines subroutines with parameter lists. You can design your own estimation routines. For example, the following computes a censored regression using the logistic distribution: It also uses MATRIX and CALCULATE to compute a set of marginal effects.
Procedure=LogitLDV(DVar,Limit,IVars) $
? Number of independent variables
Calc; Kvars = Col(IVars) $
? Binary indicator for limit and nonlimit observations
Create; Var_0 = (DVar <= Limit) ; Var_1="1" Var_0 $ ? Tobit model based on the normal distribution is used to obtain a good set ? of starting values for iterations. As part of the results of the procedure, ? we also request a full set of results for the tobit model. Tobit ; Lhs="DVar" ; Rhs="Ivars" ;MarginalEffects$ ? Compute MLEs of the logistic model using Maximize. Maximize ; Fcn="B_X" / h | E="DVar/h" B_X | R_0="B_X" Limit/h | L_0="1/(1" + Exp(R_0)) | L_1="Exp(E)/(1" + Exp(E))^2 | Var_0 * Log(L_0) + Var_1 * Log(L_1/h) ; Start="B,S" ; Labels="Kvars_B,h" $ ? Obtain marginal effects and standard errors. ? d="P1" * beta="F[(beta'x" Limit)/sigma] * beta where F="logit" CDF. ? Evaluate this at the mean of the data. To compute the asymptotic covariance ? matrix, we require the matrix of partial derivatives, ? G="[F" * I + F(1-F)beta * x'/sigma] and ? F(1-F)(-1/sigma)[(beta'x Limit)/sigma](-1/sigma) * beta' ? Then, the covariance matrix is G V G'. Matrix ; Beta="Part(B,1,KVars)" ; Xbar="Mean(IVars)" $ Calc ; KV1="KVars+1" ; Sig="B(KV1)" ; ZL="(Beta'Xbar" Limit)/Sig ; List ; F="Lgp(ZL)" ; Nolist ; ds="F*(1-F)*(-1/Sig)*ZL" ; db="F*(1-F)/Sig" $ Matrix ; Gbeta="F" * Iden(Kvars) + db * Beta * Xbar' ; Gsigma="ds" * Beta ; G="[Gbeta,Gsigma]" ; Delta="F" * Beta ; Vdelta="G" * Varb * G' ; Stat (Delta,Vdelta) $ EndProcedure
* EXECUTE invokes procedures.
* DO FOR, DO WHILE, and DO UNTIL define loops and execute commands iteratively.
* Variable lists can be indexed by number in loops.
* Commands are submitted from a screen editor with numerous options for controlling the flow of execution.
|
| LIMDEP V8.0のTopに戻る |
|
|

